İki genel bakış açısı ve biraz psikoloji:
Makine öğrenimiyle ilk karşılaşıldığında, genellikle algoritmadan algoritmaya, teknikten tekniğe, denklemden denkleme koşulur. Ancak daha sonra kişi edindiği bilgilerdeki genel eğilimler üzerinde düşünebilir.
'Öğrenmenin' ne anlama geldiği çok soyut bir kavramdır. Bu makalenin amacı, bir makinenin öğrenmesinin ne anlama geldiğine dair iki genel yorum sunmaktır. Bu iki yorum, göreceğimiz gibi, aynı madalyonun iki yüzüdür ve makine öğrenimi boyunca her yerde ele alınmaktadır.
Makine öğrenimi konusunda deneyimli olsanız bile, belirli mekaniklerden geçici olarak uzaklaşıp öğrenme kavramını soyut bir düzeyde ele almak size bir şeyler kazandırabilir.
Makine öğreniminde öğrenmenin, kayıba yönelik parametre güncellemesi ve manifold eşleme olarak adlandıracağımız iki temel yorumu vardır. Göreceğimiz gibi, bunların psikoloji ve zihin felsefesi ile önemli bağlantıları vardır.
Kayıp Yönlü Parametre Güncellemesi
Daha önce tartışılan makine öğrenimi algoritmalarından bazıları tabula-rasa yaklaşımını benimser: 'boş bir sayfa' rastgele bir tahminden başlarlar ve tahminlerini yinelemeli olarak geliştirirler. Bu paradigma bize sezgisel görünmektedir: bisiklete binmeyi öğrenmek veya cebirsel ifadeleri basitleştirmek gibi yeni bir beceri edinmeye çalışırken birçok hata yaparız ve 'pratik yaptıkça' daha iyi oluruz. Bununla birlikte, algoritmik bir bakış açısıyla, iki varlığın varlığını açıkça kabul etmemiz gerekir: bir durum ve bir kayıp.
Bir algoritmanın durumu, parametre kümesinin değerleri ile tanımlanır. Parametreler, bu bağlamda, bir algoritmanın nasıl davranacağını belirleyen statik olmayan değerlerdir. Örneğin, bowling oyununuzu optimize etmeye çalıştığınızı düşünün. Elinizde birkaç parametre vardır: bowling topunun ağırlığı, parmaklarınızın parmak deliklerindeki konfigürasyonu, bowling oynamaya hazırlanırkenki hızınız, kolunuzun hızı, bowling oynadığınız açı, bırakma anındaki spin vb. Her bowling oynadığınızda yeni bir durum tanımlarsınız çünkü bir optimizasyon algoritması olarak yeni parametreler denersiniz (daha önce oynadığınızın aynısını oynamadığınız sürece, bu durumda önceki bir duruma geri dönersiniz, ancak bu hem bowlingde hem de makine öğreniminde nadir görülen bir durumdur).
Doğrusal regresyon ve lojistik regresyondaki katsayıların her biri bir parametredir. Ağaç tabanlı modeller, derinlikleri uyarlanabilir olduğundan statik sayıda parametreye sahip değildir. Bunun yerine, bilgi kazanımı kriterlerini optimize etmek için gerektiği şekilde daha fazla veya daha az koşul oluşturabilirler, ancak bunların hepsi parametredir.
Bununla birlikte, ağaç tabanlı modeller - ve tüm algoritmalar - hiperparametrelere tabidir. Bunlar, parametrelerin kendi içinde hareket etmesi gereken sistem düzeyindeki kısıtlamalardır. Bir karar ağacının maksimum derinliği ve rastgele orman topluluğundaki ağaç sayısı hiper parametre örnekleridir. Bowling örneğimizde, meta-parametreler binanın nemini, size verilen bowling ayakkabılarının kalitesini ve bowling şeritlerinin kalabalıklığını içerebilir. Bir optimizasyon algoritması olarak, bu koşullar içinde var olursunuz ve altta yatan koşulları değiştiremeseniz bile iç parametrelerinizi (hangi bowling topunu seçtiğiniz, nasıl bowling oynadığınız vb.
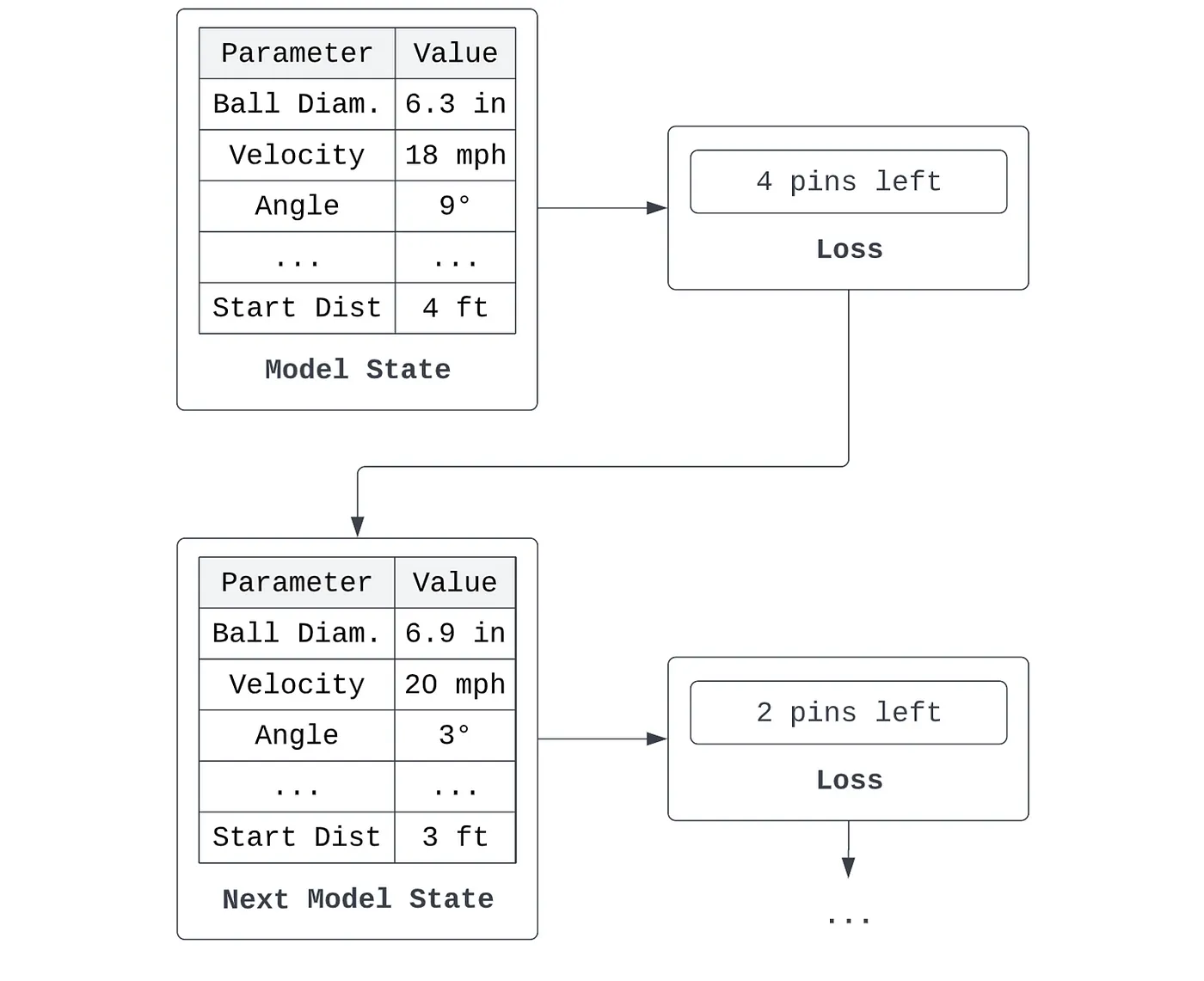
Diğer yandan kayıp, herhangi bir durumun 'kötülüğü' ya da hatasıdır. Bir kayıp, bir modelin kötülüğünün davranışından nasıl türetileceğini formüle etmelidir. Örneğin, belirli bir durumu benimsediğimi varsayalım - 6,3 inç çapında bir bowling topu seçiyorum, topu saatte 18 mil hızla, kulvar kenarlarına göre 9 derecelik bir açıyla, kulvardan dört fit uzaktan başlayarak bırakıyorum ve bu şekilde devam ediyorum - ve 6 lobut düşürüyorum. Durumumun davranışı 6 lobut düşürdüğümdür. Durumun kötülüğünü ölçmek için, tam olarak bu durum parametreleriyle serbest bırakılan bir bowling topu göz önüne alındığında, kaç lobut devirmediğimi hesaplıyoruz - 4 lobut. Kötülüğümü en aza indirmek için, bir sonraki bowling oynayışımda parametrelerimi ayarlarım.
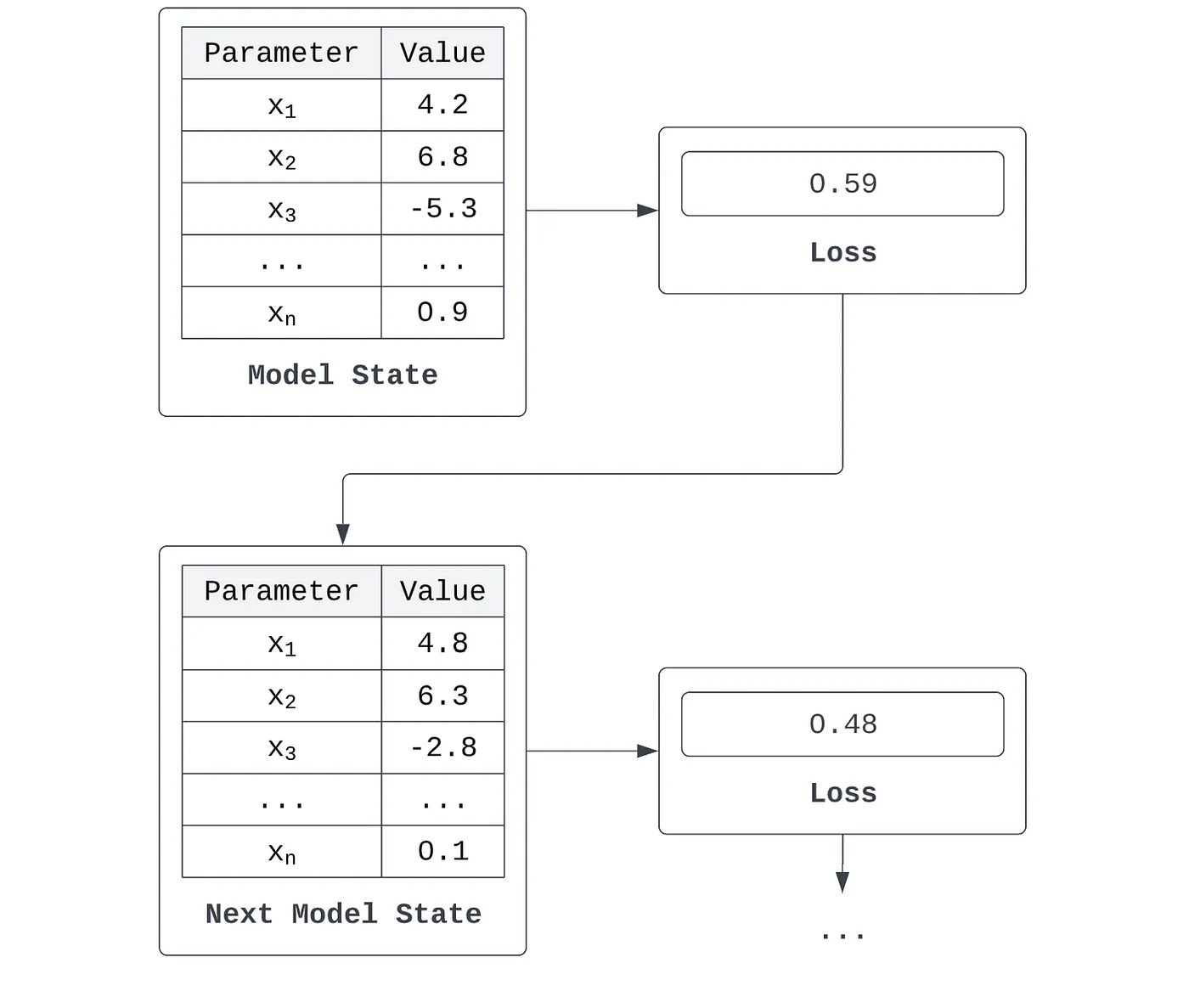
Algoritmalar açısından konuşacak olursak, durum genellikle bir girdiyi tahmine dönüştüren bir dizi katsayı veya kriterdir ve kayıp, bir modelin tahmini ile istenen çıktısı arasındaki farkın matematiksel bir ölçümüdür. Bir modelin {x_1, x_2, ..., x_n} ile gösterilen n parametresi olduğunu varsayalım. Bunlar doğrusal bir regresyon modelinin katsayıları, k-ortalamalar modelindeki kümelerin merkezi olabilir veya bir karar ağacı modelindeki ayırma kriterlerini temsil edebilir. Bu modelin bazı veri kümeleri üzerinde yaptığı bir hata türetebiliriz - örneğin ortalama karesel hata. Model, kaybını iyileştirmek için parametre setini yinelemeli olarak ayarlarsa, o zaman öğreniyor olduğunu söyleriz.
Tüm bu süreci kabaca öğrenme olarak adlandırsak da, asıl öğrenme algoritması kayıptan parametre güncellemesine dönüşümde gerçekleşir. Mevcut durumun değerlendirilmesi (yani parametreden kayba dönüşüm veya türetme) 'hissetme' veya 'akıllı' bir süreç olarak düşünülebilir.
Psikolojik ve evrimsel olarak bilgilendirilmiş bir hipotez, insanlar olarak sürekli olarak kayıp odaklı parametre güncelleme paradigması yoluyla öğrenen modellerinkine kavramsal olarak benzer bir optimizasyon oyunu oynadığımızı öne sürmektedir: sürekli olarak durumumuzun 'kötülüğünü' gözlemliyoruz ve durumumuzu ayarlayarak kötülüğü iyileştirmeye çalışıyoruz. Bununla birlikte, kötülük ölçütlerimiz ortalama-kare-hata hesaplamasından daha karmaşıktır: aynı anda içsel ve dışsal, içgüdüsel ve hesaplanmış çeşitli sinyallerle hokkabazlık yapıyoruz ve bunların hepsini mevcut değişken özelliklerimizle ilişkili olarak anlamlandırmaya çalışıyoruz. Örneğin, bowling oynarken, deneseniz bile doğrudan devirdiğiniz pin sayısını optimize etmeye çalışmıyor olabilirsiniz. Bunun yerine, sosyal kaygıyı en aza indirmeye veya randevunuzdan ya da arkadaşlarınızdan ne kadar etkilendiğinizi en üst düzeye çıkarmaya çalışıyor olabilirsiniz; bu da devrilen lobut sayısını en üst düzeye çıkarmakla aynı optimal durum konfigürasyonuyla sonuçlanmak zorunda değildir.
Bu fikri akılda tutmak - kendi davranışımızı, durumlarımızın kötülüğüne ilişkin değerlendirmelere yanıt olarak değişken durumların sürekli güncellenmesi olarak görebileceğimiz - kayba dayalı parametre güncellemesinin nasıl davrandığına ilişkin sorunları ve olguları daha iyi anlamamızı sağlar. Birincisi, insanlar durumlarını sürekli olarak değerlendiriyor olsalar bile durumlarını her zaman değiştirmiyorlar. Bu durum yakınsamayı gösterir - bu insanlar, durumlarında uygulanabilir hiçbir değişikliğin kötülüğü azaltmayacağı bir dizi duruma ulaşmışlardır.
Alternatif olarak, bazı insanlar ne yazık ki bağımlılık (madde, kumar, sosyal medyada gezinme vb.) ya da felç edici paranoya (finansal borca girme, değerli eşyalarını kaybetme, saygınlığını yitirme, büyük kalabalıklar ve benzeri) nedeniyle kötü koşulların yinelenen yıkıcı davranışlarına hapsolmuştur. Öğrenmenin teknik dilinde bunlara yerel minimumlar diyoruz. Bunlar, ajanların vardığı ve ya orada kalmanın ondan hemen uzaklaşmaktan daha kolay olduğu için (örneğin bir bağımlılıktan kurtulmak) ya da eşdeğer olarak, hemen uzaklaşmanın kalmaktan daha kötü olduğu için (yani bir değişiklik durumunda kişinin durumunun zarar görmesi veya kötüleşmesi paranoyası) ayrılmamayı 'seçtiği' yakınsama yerleridir.
Algoritmalar, elbette insana daha az benzer şekillerde olsa da, genellikle benzer davranışlar sergiler. Kayıp yönelimli parametre güncellemesinde kayıp ve durum arasındaki ilişkiyi genellikle bir kayıp manzarası fikri aracılığıyla geometrik ve nicel bir şekilde kavramsallaştırırız. Kayıp manzarası, her parametre için bir ekseni ve kayıp için ek bir ekseni olan geometrik bir uzaydır. Kayıp alanı, her bir parametre değeri kümesini o kayıp için ortaya çıkan bir kayıp değeriyle eşleştirmemizi sağlar.
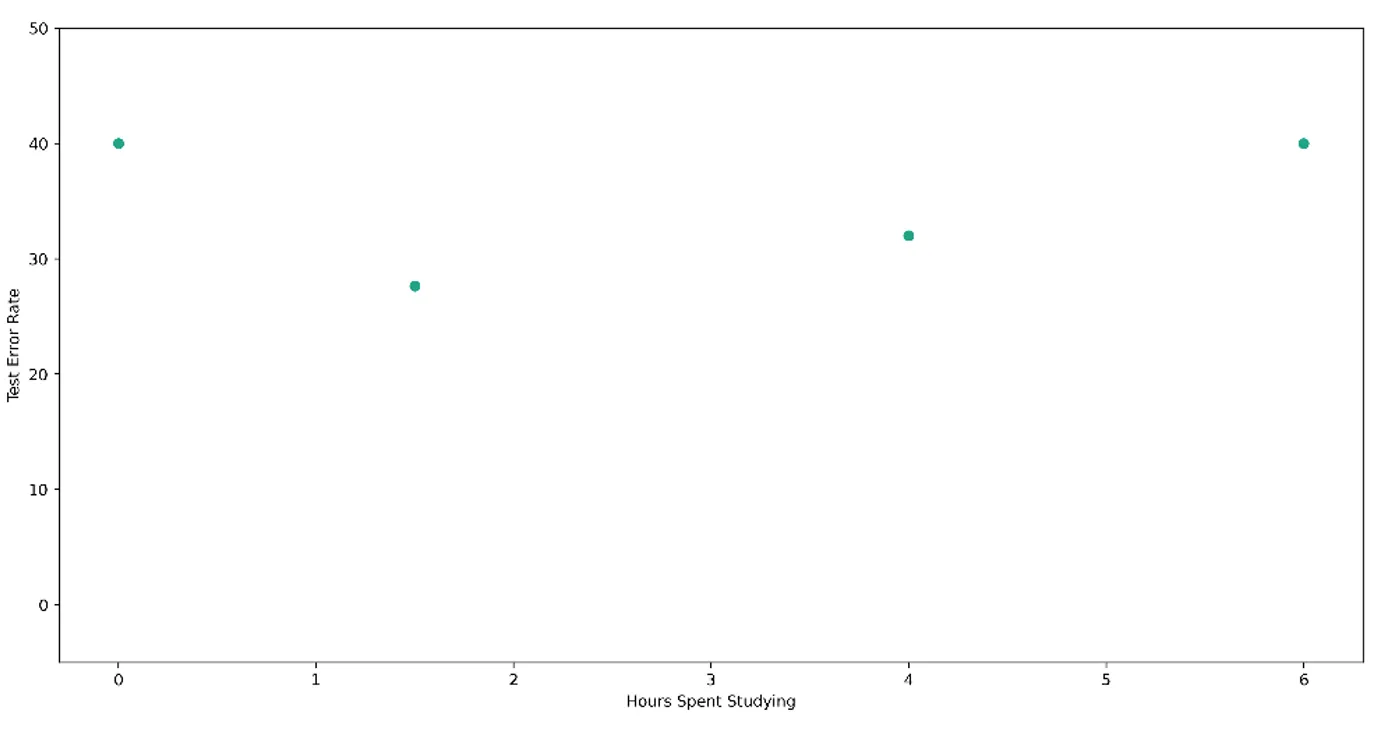
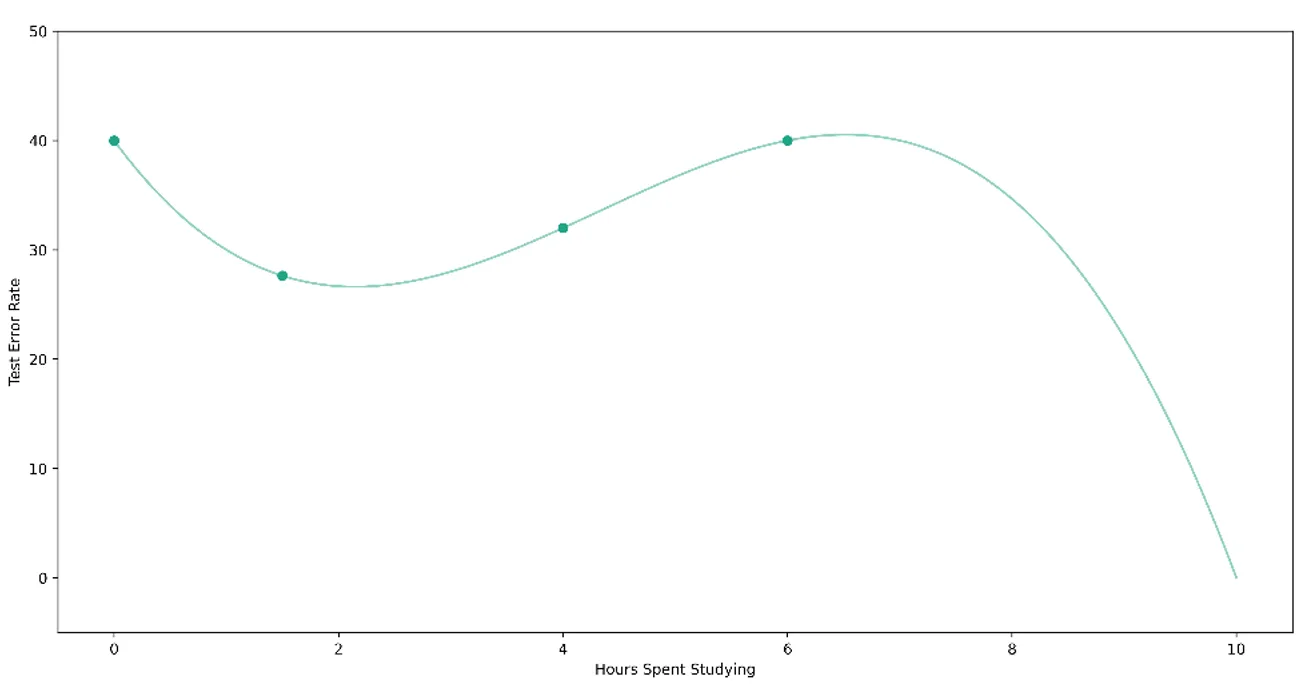
Bu önemli kavramı açıklamak için, bir test için en uygun çalışma stratejisini öğrenmeye çalıştığınızı varsayalım. Sadece bir parametreyi öğrenme problemini ele alacağız - test için kaç saat çalıştığınız. Daha önce dört sınava girdiğinizi varsayalım, yani - örnek olması açısından bu testlerin çevresel olarak karşılaştırılabilir olduğunu varsayarsak - öğrenebileceğiniz dört veri noktanız var. Bu dört testin her biri için farklı sayıda saat çalıştınız ve buna bağlı olarak farklı performanslar elde ettiniz: hiç çalışmadığınızda %60, 1,5 saat çalıştığınızda yaklaşık %75, 4 saat çalıştığınızda yaklaşık %70 ve 6 saat çalıştığınızda yaklaşık %60. Bunları, geleneksel olarak daha küçük olduğunda daha arzu edilir olma özelliğine sahip olan kaybın (bu durumda hata oranı (bir eksi performans) olacaktır) optimize edilen parametre ile nasıl değiştiğini göstererek aşağıdaki gibi çizeceğiz.
Bu bilgiyi kullanarak, en küçük hata oranını elde etmek için çalışılacak en uygun saat sayısını bulmak istiyoruz. Şu ana kadar topladığımız bilgilere göre, optimum parametre değeri iki saate yakın bir yerde olacak gibi görünüyor. Ama nasıl emin olabiliriz? Yakın cevaplar ya da uzak cevaplar hakkında nasıl düşünebiliriz? Verilerimize bakma ve minimum kayıp arama sürecini nasıl karakterize edebiliriz?
Kayıp manzarası, fiziksel ve niceliksel anlamda öğrenme hakkında düşünmemize yardımcı olan kavramsal bir araçtır. Her parametre değeri ile buna karşılık gelen hata oranı arasındaki kesin, gerçek ilişkiye erişimimiz olduğunu hayal ediyoruz. Bu, parametre-kayıp uzayımız boyunca bir eğri veya 'manzara' çizmemizi sağlar. Bilinen noktaların her birini manzaradan 'örneklenmiş' olarak anlayabiliriz. Pratikte bu manzaraya erişimimiz olmadığı tekrarlanmalıdır. Bu daha ziyade muhakeme ve anlamaya yardımcı olacak teorik bir modeldir.
Şimdi, iki boyutlu bir dünya tepesine baktığınızı hayal edin. Bu tepenin yüzeyinde duran ve en düşük rakımlı yeri arayan küçük bir gezgin olduğunuzu varsayalım. İstediğiniz gibi hareket edebilirsiniz - ışınlayıcınızı kullanabilir ve her yere rastgele atlayabilirsiniz, yavaş adımlar atabilir, büyük sıçramalar yapabilirsiniz. Bu tepeyi keşfederken, ziyaret ettiğiniz yeni yerlerin hiçbirinin daha önce ziyaret ettiğiniz en düşük yerden daha alçak olmadığını görebilirsiniz. Bir miktar sonuçsuz keşiften sonra, daha önce ziyaret ettiğiniz en düşük konumla yetinmeye karar verebilirsiniz. Bu yakınsama olduğunu gösterir.
Algoritmalar, kayıp manzarasını nasıl kullandıklarına ve bu manzarada nasıl gezindiklerine göre farklılaştırılabilir. Her algoritmayı kendi gezgin kişiliği olarak düşünebilirsiniz. Aptal bir öğrenme algoritması, parametreleri çok sayıda kez rastgele değiştirmek ve en iyi performans gösterene geri dönmektir - rastgele arama. Bu, biraz fazla içmiş olabilecek, ışınlayıcılarıyla kayıp manzarasının her yerine atlayan düzensiz bir gezgindir.
Alternatif olarak, muhafazakar bir öğrenme algoritması, her bir parametre değeri setini belirli bir granülerlikle aramak olacaktır. Bu çok gayretli ancak verimsiz bir gezgindir; kayıp manzarasının her bir 'santimini' yavaşça yürür, notlar alır ve titiz ölçümler yapar.
Daha akıllı bir gezgin, belirli bir kararı verirken elde edeceği kazanç için ölçütler geliştirmeye çalışabilir ya da üzerinde durduğu zeminin eğimini analiz ederek hangi yönün en hızlı inişi sağlayacağını belirleyebilir.
Kayıp manzarası, öğrenme algoritmasının 'yakındaki' çözümlere kıyasla en iyisi gibi görünen, ancak diğer bazı 'küresel' minimumlardan daha kötü olan bir çözüme yakınsadığı yerel minimumlar gibi olguları da dikkate almamızı sağlar. Önceki örneğimizde, ders çalışmak için harcanan saat sayısını optimize ederken, iki saat ders çalışmayı yerel bir minimum olarak tanımlayabiliriz. Bu, diyelim ki yarım saat veya dört saat çalışmaya kıyasla daha yüksek bir sınav hata oranı sağlayacaktır. Ancak, gerçek küresel minimum 10 saat çalışmaktır ve bu da bize sıfır gibi mükemmel bir sınav hata oranı verir. Yerel minimumları bir görme problemi olarak düşünün: engebeli bir arazide yol alan bir gezgin sadece önündeki dağları görebilir ama ötesindeki daha derin vadileri göremez ve hemen önündeki sığ vadinin yeterli olacağına karar verir.
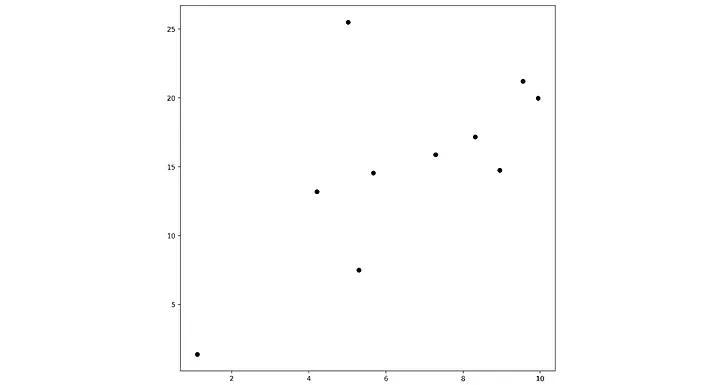
Pragmatik bir örnek düşünün. Y = mx doğrusunu kontrol eden tek bir m parametresi olan çok basit bir modelimiz var ve bir nokta veri kümesine en iyi uyan (yani doğru ile nokta arasındaki ortalama farkı en aza indiren) m değerini bulmak istiyoruz.
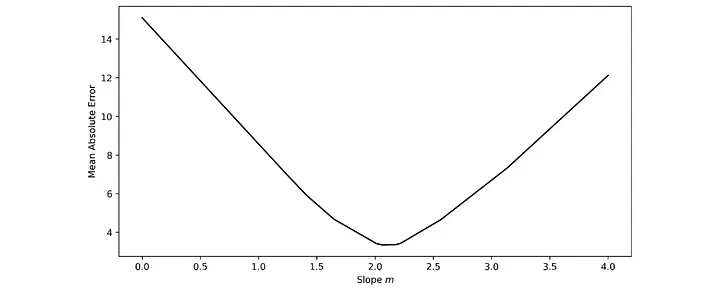
Kayıp manzarası, 0 ila 4 arasındaki eğim değerleri için aşağıdaki gibi görünür.
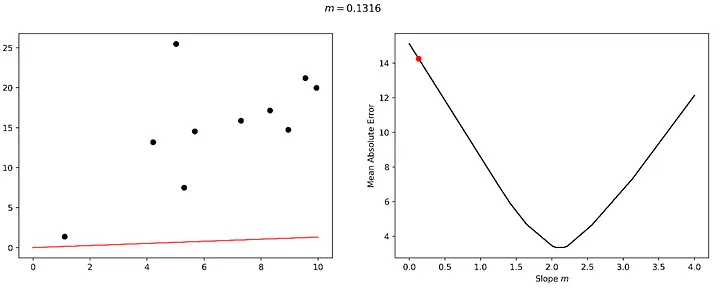
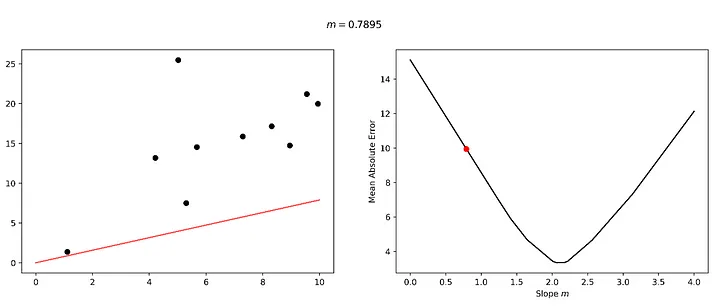
Bu kayıp manzarasını gezme sürecini ve modelimizin ince ayarı üzerindeki karşılık gelen etkiyi ele alalım. Bu manzara üzerinde 0,1316 gibi çok küçük bir eğim değeriyle başlayacağız. Bu değerin veri setimiz için mükemmel bir uyum olmadığı açıktır ve buna bağlı olarak kayıp manzarasında 'çok yüksek bir zeminde' bulunmaktayız.
Hadi "öğrenelim". Diyelim ki biraz 'sağa' bakıyoruz ve buna bağlı olarak daha alçak bir zemin buluyoruz.
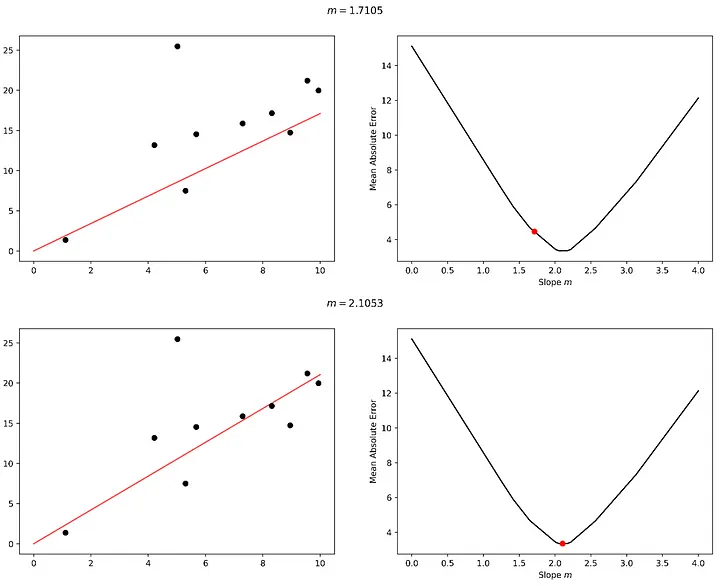
Yolculuğun başarılı ilk ayağından cesaret alarak, aynı yönde iki kez daha adım atacağız ve 2.1053 eğimli bir model kullanarak minimum hataya ulaşacağız.
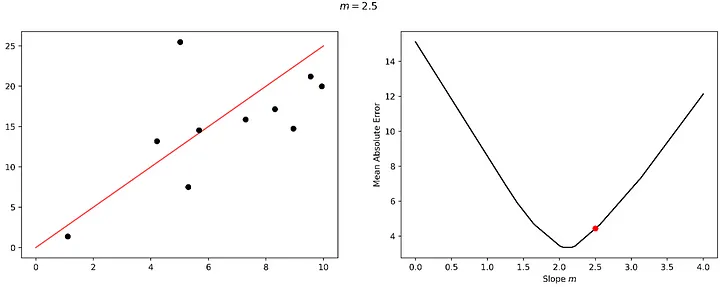
Diyelim ki bir adım daha attık ve kayıp manzaramızı alçaltmak yerine tırmanmaya başladık, bu da daha kötü bir modelle sonuçlandı. İşte bu noktada öğrenmemiz bir hataya düşmüştür; ya keşfetmeye devam etmek (ve belki daha aşağıda daha iyi bir çözüm bulmak) ya da önceki en iyi çözüme geri dönmek isteyebiliriz. Bu, öğrenme sürecinde bir hata ve düzeltmedir.
Ancak pratikte makine öğrenimi modelleri bir parametreden çok daha fazla parametreye sahiptir. En basit model türü olan doğrusal regresyon modeli bile veri kümesindeki değişken sayısı kadar parametreye sahiptir.
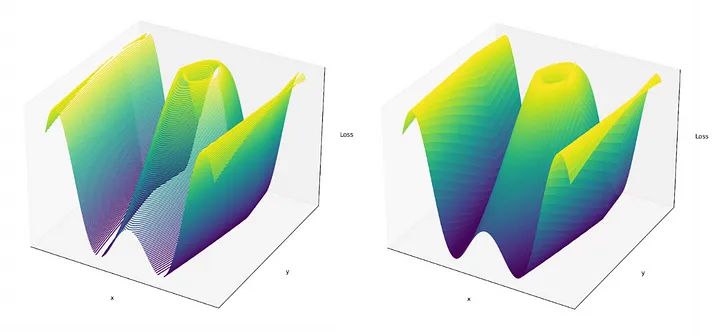
Bu fikri, biraz daha az sezgisel olsa da, daha yüksek boyutlu uzaylara genelleyebiliriz. Örneğin, bunun yerine iki parametreli bir model düşünün. İki parametre değerinin her kombinasyonunun belirli bir kayıpla nasıl eşleştiğini gösteren kayıp manzarası buna uygun olarak üç boyuta sahip olacaktır. Artık gezinmeye çalıştığımızı hayal edebileceğimiz üç boyutlu bir 'manzaramız' var.
Çoğu modern makine öğrenimi modelinin düzinelerce, yüzlerce ve hatta milyarlarca (derin öğrenme durumunda) parametresi vardır. Kavramsal olarak öğrenme süreçlerini - "makine öğrenimi" veya "derin öğrenme "deki "öğrenme" - ilgili düzinelerce, yüzlerce ve milyarlarca boyutlu kayıp manzaralarında gezinme, tepeler boyunca "en düşük zeminin yerini", kaybı en aza indiren parametre değerlerinin kombinasyonunu arama olarak anlayabiliriz.
Manifold Haritalama
Kayıp Yönlü Parametre Güncellemesi, öğrenmeyi anlamanın sezgisel bir yoludur: dahili parametrelerimizi, dahili veya harici olarak (örneğin bir çevre tarafından) değerlendirilebilen geri bildirim sinyallerine yanıt olarak güncelleriz. Kayıp manzarası kavramı, soyut öğrenme problemini daha fiziksel bir alana çevirmemize olanak tanır ve öğrenme sürecinde gözlemlenen, vasatın altındaki durumlara (yerel minimumlar) yakınsama gibi olgulara somut açıklamalar sunar.
Kayıp Yönlü Parametre Güncellemesi model merkezli bir öğrenme yorumudur: kayıp manzara uzayı fiziksel olarak modelin bileşenleri (parametre değeri eksenleri) ve bu bileşenlerin toplam performansı (kayıp ekseni) tarafından tanımlanır. Öte yandan, Manifold Eşleme yorumu veri merkezlidir. Öğrenmeyi bir ajan olarak model açısından tanımlamak yerine, öğrenmeyi veri içinde gerçekleşirken gözlemleriz. (Elbette, göreceğiniz gibi, bunlar aynı madalyonun iki yüzüdür).
2001: A Space Odyssey filmindeki bir rol için büyük kardeşine tercih edilmediği için hala acı çeken Hal 9001'in bakıcısı olduğunuzu varsayalım. Hal 9001'in bakıcısı olarak sorumluluklarınızdan biri Hal'in bugünkü sıcaklıktan memnun olup olmayacağını tahmin etmektir. Elinizde önceki sıcaklıklar ve Hal 9001'in buna karşılık gelen memnuniyeti hakkında bazı veriler var. Bugünün sıcaklığı 64 derece. Hal 9001'in memnun olup olmayacağını tahmin edebilir misiniz?
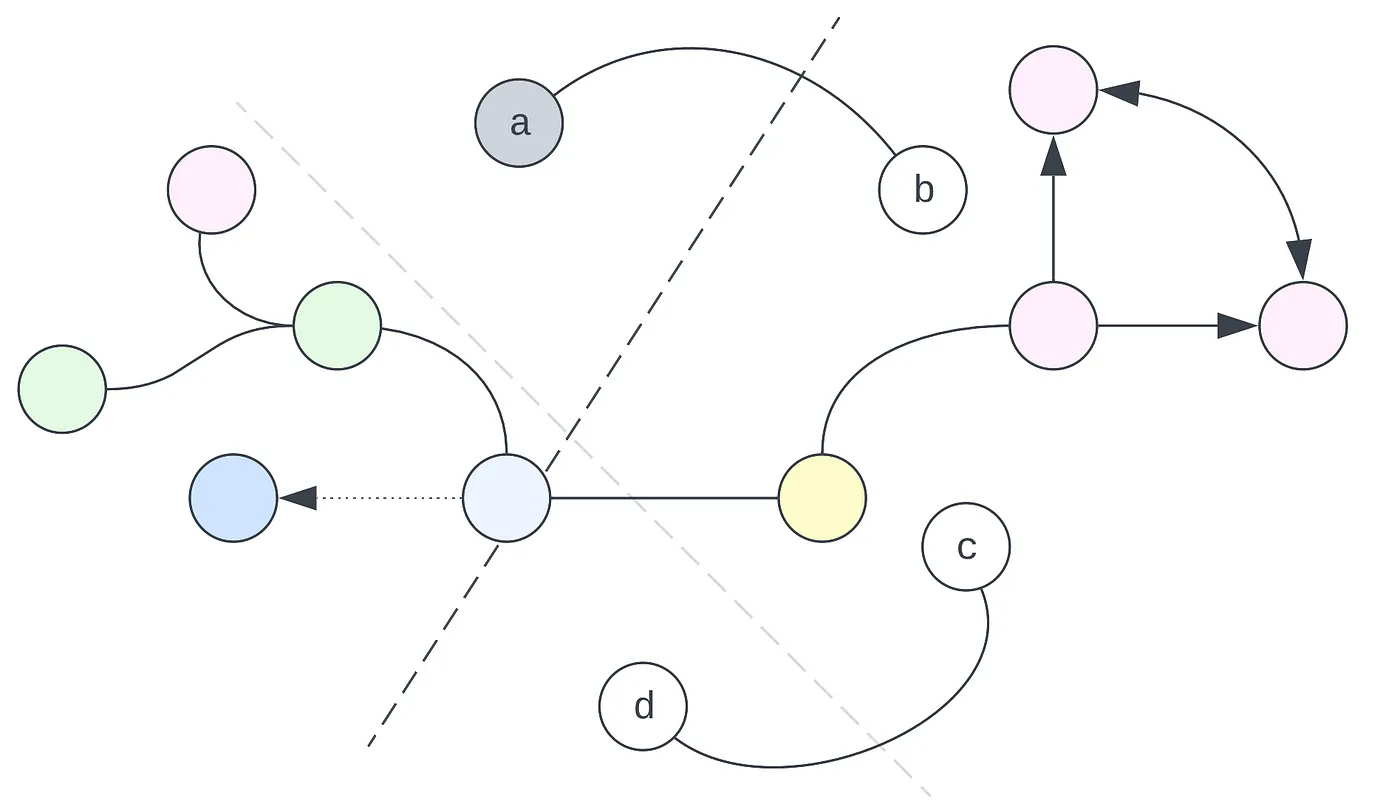
Verilere bir göz attığımızda Hal 9001'in (şükürler olsun ki) karşılanacağını görüyoruz. Bu çıkarımı nasıl yaptınız? Özellik uzayında dolaylı olarak bir manifold inşa ettiniz. Buradaki verilerimiz yalnızca bir özelliğe, sıcaklığa sahip olduğundan (Hal 9001'in memnuniyeti bir özellik değil, hedeftir), özellik uzayının yalnızca bir boyutu vardır. Bu da bir sayı doğrusu anlamına gelir:
Daha açık bir ifadeyle, verileri bir nokta boyunca ayırmak için bir manifold çizebiliriz. Bu durumda, aşağıdaki manifoldu çizerek verileri mükemmel bir şekilde ayırabiliriz:
Buradaki en önemli içgörü, manifoldun sadece özellik uzayında kapladığı ince 'şerit' ile ilgili olmadığıdır: bunun yerine, tüm özellik uzayını etkiler. Hangi alanların hangi sınıflara ait olduğunu tanımlar. Dahası, daha önce görmediğiniz noktalar üzerinde nasıl çıkarım yapacağınızı tanımlar. Bu özellik uzayında '64' noktasını işaretleyecek olursak, 'Evet' memnuniyet kategorisine girdiğini görürüz.
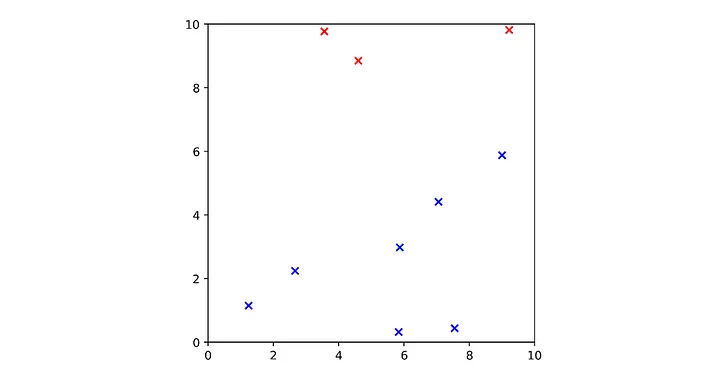
Verileri ayırmak için aşağıdaki manifoldu çizebiliriz. Veri kümesine mükemmel bir şekilde uymaktadır; yani verileri kendi sınıflarına mükemmel bir şekilde ayırmaktadır.
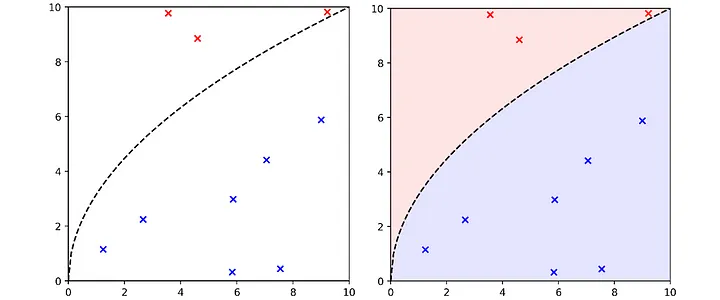
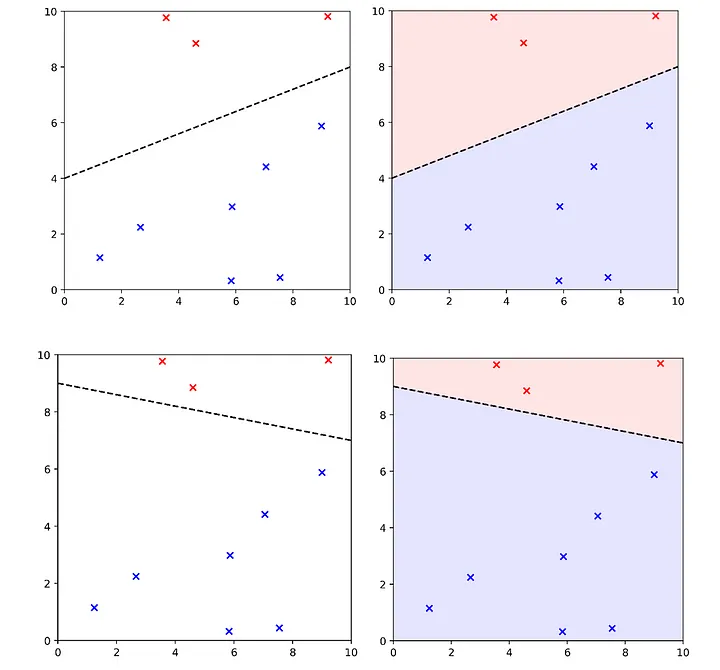
Bununla birlikte, başka birçok geçerli manifold da çizebiliriz. Bunlar da verileri mükemmel bir şekilde ayırır.
Bu manifoldların hepsi, özellik uzayında farklı sınıftaki öğeleri ayırmada eşit derecede mükemmel performans elde etmeleri bakımından aynı eğitim seti performansına sahip olsalar da, tüm özellik uzayını nasıl etkiledikleri konusunda belirgin farklılıklar gösterirler. (1, 7) koordinatındaki nokta, manifoldun farklı bir yöne sahip olması nedeniyle üstteki eşlemede alttaki eşlemeden farklı bir sınıf olarak sınıflandırılacaktır.
Benzer şekilde, tek boyutlu örneğimize dönecek olursak, sınırımızı bilinen verileri ayırmada eşit derecede iyi olacak farklı şekillerde çizebilirdik.
Bu da yeni veriler için nasıl karar verdiğimizi etkiler. Diyelim ki hava 55 derece; üst manifold Hal 9001'in tatmin olacağını öngörüyor ama alt manifold Hal 9001'in tatmin olmayacağını öngörüyor.
Bu tür bir keyfilik, üzerinde düşünülmesi gereken önemli bir konudur. Herhangi bir sorun için sistem tarafından öğrenilebilecek eşit derecede iyi birçok farklı çözüm olduğunu gösterir. Ancak genellikle modelin bir 'gerçek manifold' öğrenmesini isteriz. Bu, sadece veri kümesindeki bilinen noktaları değil, toplayabileceğimiz tüm noktaları mükemmel bir şekilde (veya en azından en iyi şekilde) ayıran 'gerçek manifold' olarak hayal ettiğimiz şeydir. Bu kavram, veri topladığımız olguya ayrılmaz bir şekilde bağlıdır.
O halde öğrenme süreci, özellik uzayındaki farklılıkları genelleştirmektir; özellik uzayı boyunca kıvrılan manifoldu, farklı veri noktalarını anlamlı bir şekilde ayıracak şekilde çizmektir. Bu süreçte, veri kümesindeki genel kuralları öğreniriz.
En önemlisi, öğrenmenin manifold haritalama yorumu, öğrenmenin veri kümesini nasıl 'etkilediğini' vurgulamamıza yardımcı olur. Model yalnızca sonlu sayıda nokta üzerinde eğitilmiş olsa da, aslında özellik uzayındaki her noktayla ilgili olduğunu anlıyoruz. Bu nedenle, manifold haritalama yorumu, modellerin nasıl genelleştiğini anlamamızı sağlar - özellik uzayında verileri ucuza ayırmak için altta yatan gerçek olguları doğru bir şekilde yansıtmayan kısa yolları öğrenmek yerine öğrenmelerini istediğimiz kuralları ('gerçek manifold') nasıl öğrendiklerini.
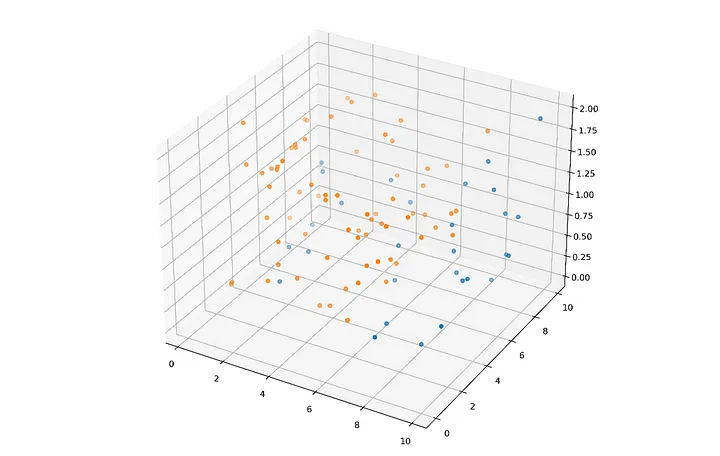
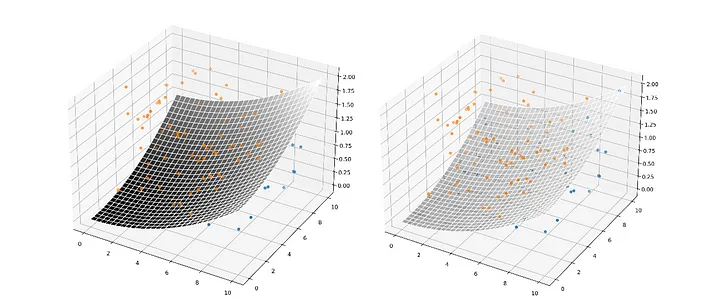
Üç boyutlu bir manifold haritalama örneğini ele alalım:
Bu noktaları ayıran üç boyutlu uzaydaki bir manifold, kelimenin daha bilinen anlamıyla bir 'yüzey'dir; uzayın üzerine örtülen bir battaniye gibi davranır, özellikler arasındaki gerçek anlamlı ilişkiler (ideal olarak) özellik uzayı boyunca yörüngesindeki her yay ve eğride kendini gösterir.
Bu karmaşık bir fikirdir. Kayıp yönelimli parametre güncelleme yorumundan daha az sezgiseldir, ancak üzerinde düşünülmesi gereken önemli bir fikirdir.
Psikoloji ve Zihin Felsefesinden Katkılar
Kayba yönelik parametre güncelleme yorumu, öğrenmeyi bir kayba veya mevcut durumun kötülüğünü tanımlayan geri bildirim sinyaline yanıt olarak dahili bir durum kümesinin yinelemeli olarak güncellenmesi olarak tanımlar. Manifold haritalama yorumu, öğrenmeyi özellik uzayında farklı veri noktalarını en iyi şekilde ayıran ama aynı zamanda görünüşte tüm uzay boyunca 'tahminler' (genellemeler) yapan bir manifoldun (karar sınırı, yüzey) oluşumu olarak tanımlar.
Bunlar, bu bağlamda öğrenme sürecini yorumlamanın makul ve hatta belki de doğal yolları gibi görünmektedir. Ancak, bunlar 'öğrenme' kavramının ağırlıklı olarak matematiksel, teknik ve soyut tanımları olsa da, böyle bir tanımın hala belirli bir felsefi perspektifi veya dünya görüşünü onayladığını veya buna uygun olduğunu kabul etmek önemlidir.
'Öğrenmenin' ne olduğu, 'öğrenmenin' ne anlama geldiği konusunda birçok farklı felsefi duruş ve teori vardır. Yaygın bir yanılgı, matematik ve fen bilimleri gibi alanların görünürdeki iç tutarlılığını (ki daha yakından incelendiğinde aslında o kadar da tutarlı olmadığı görülür) örtük 'nesnellik' ve 'hakikat' etiketleriyle ilişkilendirmektir. İlerleyen bölümlerde daha ayrıntılı olarak inceleyeceğimiz üzere, bu yanlış kanı genellikle YZ gibi hesaplamalı veya matematiksel sistemlere yanlış veya aşırı güven duyulmasına yol açmaktadır.
YZ'nin çeşitli örtük felsefi varsayımlarını tanımlama sürecine, 'öğrenmeye' felsefi olarak nasıl yaklaşıldığını ve kayba yönelik parametre güncelleme ve manifold eşleme yorumlarının hangi yollara uyduğunu kısaca anlayarak başlıyoruz.
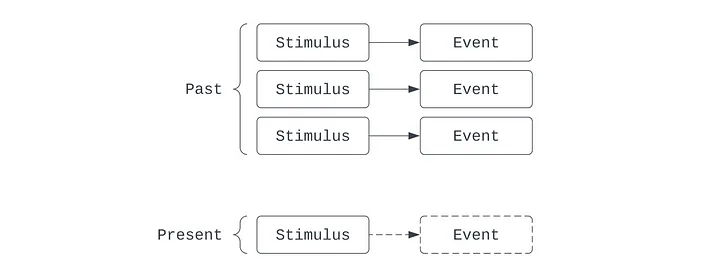
Çağrışımcılık, on sekizinci yüzyılda Locke ve Hume'dan Yapay Zeka ile olan ilişkisindeki modern önemine kadar uzun bir gelişim geçmişine sahip bir öğrenme teorisidir. Organizmaların nedensel çıkarımlar geçmişine dayanarak öğrendiklerini öne sürer: kendilerine sunulan dünyayı deneyimleyerek, daha önce bir şekilde bağlantılı olan iki olguyla sık sık karşılaşmışlarsa, bazı olguları diğer bazı olgularla ilişkilendirmeye başlarlar.
Örneğin, Isaac ne zaman bir elmayı havaya atsa, elma geri düşer. Çağrışımcı mercekte, Isaac bir parça öğrenilmiş bilgi geliştirmiştir: elma her havaya atıldığında geri düşer. Isaac birkaç kez havaya portakal atabilir ve onun da her seferinde geri düştüğünü fark eder. Aynı rutini başka nesnelerle de denedikten sonra, Isaac ilişkilendirmeyi genelleştirmeyi öğrenecektir: havaya atıldıktan sonra geri düşme özelliği elma nesnesine değil, genel olarak nesnelere özgüdür.
Çağrışımcılar tek bir temel zihinsel süreç olduğunu öne sürmektedir: fikirlerin deneyim yoluyla ilişkilendirilmesi. Ivan Pavlov'un psikoloji alanındaki çalışmaları belki de çağrışımsal öğrenme lehine en iyi bilinen kanıttır. Pavlov'un köpekleri et kokusuyla karşılaştıklarında otomatik olarak salya salgılıyordu, çünkü et kokusu (yemeden önce) ile salya salgılama arasında tarihsel olarak kurulmuş bir ilişki vardı.
Daha popüler kültürde Jim, The Office'te Dwight'a karşı çağrışımsal öğrenme süreçlerini kullanır. Jim bilgisayarını her yeniden başlattığında - ikonik Windows 'iş istasyonunun kilidini aç' sesini çalarak - Jim Dwight'a bir nane şekeri teklif eder. Dwight her seferinde kabul eder, öyle ki sesi duyduğunda içgüdüsel olarak elini uzatır. Bir gün Jim bilgisayarını yeniden başlatır ve Dwight rutin nane şekerini bekleyerek elini uzatır. Jim Dwight'a ne yaptığını sorar, Dwight da "Bilmiyorum" diye cevap verir - sonra yüzünü buruşturur ve ağzının tadının neden aniden bu kadar kötü olduğunu sorarken tükürüklü ağız sesleri çıkarır.
Pavlov'dan sonra Edward Thorndike 1911 yılında "Etki Yasası "nı öne sürmüştür. Bu yasa, bir tatmin duygusuyla ilişkilendirilen davranışların, o davranışın tekrarlanmasına yol açacağını öne sürmüştür. Etki Yasası, Pavlovcu pasif çağrışımsal öğrenmenin ötesine geçerek aktif öğrenmeye yönelir: bir organizma, memnuniyet veya ödülü en üst düzeye çıkarmak için aktif olarak davranışlarda bulunur (veya bunları bastırır). Örneğin köpeklerin iyi davranışlarının eğitiminde kullanılan mantık budur: köpeğe istenen davranış için bir ödül (ve kötü davranış için bir ceza, ki bu muhtemelen ödülün olumsuzlanmasıdır) sunulur.
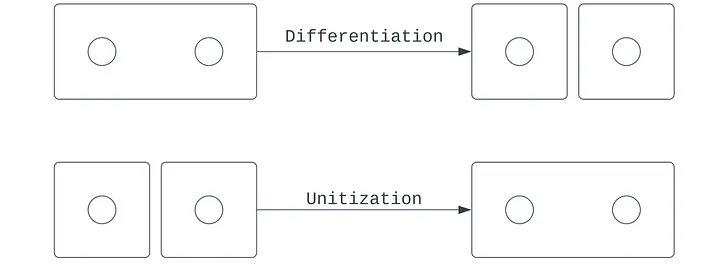
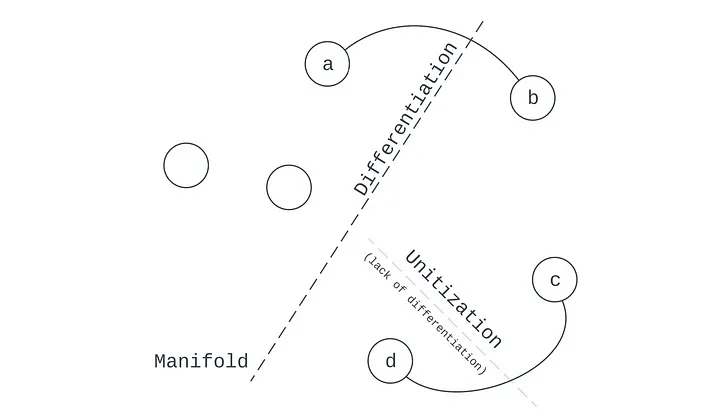
Öğrenmenin manifold haritalama yorumu, farklılaştırma ve birimleştirme ikili kavramlarının doğrudan matematiksel bir benzeridir. Manifoldun amacı en açık şekilde uzayı ayırmak, ama aynı zamanda hangi uzayın ayrılmayacağını belirlemek, yani birleştirmektir.
Sonuç yerine
Öğrenmeyi kayba yönelik parametre güncellemesi olarak düşünebiliriz - bir ajan hatayı en aza indirmek için çeşitli serbest değişkenleri ayarlamaya çalışır - ve ayrıca manifold haritalama olarak - gözlemsel uzayda geçerli olan genel kuralları keşfetmek, böylece bazı örnekleri ayırırken diğerlerini birleştirmek. Gördüğümüz gibi, bu iki yorum aynı madalyonun iki yüzüdür: biri model merkezli, diğeri ise veri merkezlidir. Her ikisi de makine öğreniminde yaygın olarak kullanılsa da, davranış bilimleri gibi diğer alanlarda da kullanım alanları bulabiliriz.
https://tinyurl.com/mwmw7fds

Hiç yorum yok:
Yorum Gönder